Мани менеджмент на форекс калькулятор торгового лота + видео Портал TradeLikeaPro

Если посадить двух начинающих трейдеров напротив друг друга и сказать, чтобы они открывали противоположные сделки, то они с вероятностью 99% проиграют. Если же в аналогичной ситуации открывать противоположные сделки будут профессиональные трейдеры, то каждый из них заработает. И дело здесь не в особенной стратегии, а в соблюдении простых правил мани-менеджмента. Чтобы этого не произошло, необходимо запомнить универсальные правила мани-менеджмента, которые можно применять в любой стратегии. Один простой способ измерить волатильность – это использовать полосы Боллинджера, которые отображают стандартное отклонение для оценки возможных различий в движении цены.

Методы включают в себя фиксированный лот, процент, пропорцию и максимальный лот. Стратегический money management – это долгосрочное планирование управление собственным капиталом. Подразумевает под собой анализ макроэкономических показателей, политических событий, финансовых новостей, выбор оптимального соотношения финансовых инструментов и осуществление управления. Для минимизации торговых рисков вы должны иметь стратегию, подтвержденную тестированием на истории и торговой практикой на демо-счетах.

Естественно, он зависит от общего финансового состояния трейдера и его торговых навыков. В любом случае, месячная потеря не должна психологически травмировать трейдера и вводить его в тильт (неустойчивое психологическое состояние). Именно эти вопросы трейдер должен проработать для себя до входа в рынок и четко следовать им на протяжении всего торгового процесса. Если торговая стратегия определяет точки входа в рынок, то риск-менеджмент определяет точки выхода из него. Правила управления капиталом появились, наверное, одновременно с возникновением товарно-денежных отношений, но основные принципы мани менеджмента были сформулированы не более века назад. Как уже не единожды говорилось, торговля на финансовых рынках является высокорискованным родом деятельности, а чтобы добиться успеха в трейдинге, следует минимизировать потенциальные риски.

<img class='aligncenter' style='display: block;margin-left:auto;margin-right:auto;' src="data:image/jpeg;base64,iVBORw0KGgoAAAANSUhEUgAABNgAAAIXCAMAAAB5BhMVAAAABGdBTUEAALGPC/xhBQAAAAFzUkdCAK7OHOkAAAAJcEhZcwAADsQAAA7EAZUrDhsAAAMAUExURf///3N8iP/Mhv/prgwXKampqba0tn2GlPLy8gKm8qvp/1ev6sn/////6o3M/6WlpeivZf//0Oj///8BAcmSKQyS0FeS0MmSZatfho1frqtfKczMzMPGywxfrvf399jZ2gwXZVcWKdLS0+Hi4gwXhvDx8eXm59PV16tfZfz5+o0WKNzd3/r+/n9+flpaWurr68qRhpWWlcHDw40Xhu3//42w6jIxMVderru7vXV1de3t8YWFhY7T/8rN0VUWhguAQ5i3yf/Sjej/6qqElI2R0fT19dT//0SeWf//5r+3q7XDweivh6yQr32vw8G6uH2Guf//+aOjpH2gv8Lq/v//2LGglOu1bqq6y6Po/5mGlMr/61ZfZmy17ZLJ6rWvlP7Wo+rGl4wYZKPX/On/0SpBUUdQT//stP4lJbO3vf/ty0hQXbTEy/7z8cv/0eD+/yUXKunmr+zPCqytsv/ks6uwhc/v/42Ria3p6jmX0Z5aLQwxSUc5Lq7g/P/9yNWqgVQWYv3j4n2Eqsrpr/u9un2n2AAAAP/241iy51ZdKk2n5LLs/8D5//7mphCGq/2mpiWKweMlKwtiaSU9avjGgv/+8bJsMleSrunMhvqTlP5HR3+SxP7Q0jVegXnI9KqNRODw6gwXOvfgyadPADltrmFqdRI5gytfpoxsstbg9PhmYv18fJGHqnRaOnh4eDo6juSnUazp0MF9LFaCjhZ0uwWGxguf0IU0Mq2Uf5iPvT+/9s+rZV6n0o3K0gpKomssMDU4QhwmM+NCQJFGKgbc/IyvrdCEPLF7VwkRTz0XK8mfQwxapiSx9Hi85QK4+K3Rrol4Q2A8MLJsjJGVZ/+ZJseHAFzG92VjYWDk/uT0/monaePP099RVocAT9GaRqGm8m+N0mCISclGJ0CmcP+kUX/R+29vbdaJbFavsUp+uW+m877Y8MrKhW61lad/f8uTTLrz/c2GmPXYTJVJUmtpsQAAh41leu3/6paHKaDHpOryvsmWzOGYgHqYgkum9d7/6jNsbAfJK2cAACAASURBVHja7J1faFTZHccPQrJB4gTz0IIjEW9IhpjcG++spTO9sEPYziYlFhxig/uQZgi0EHChGWWID0kjSVYCSVWwXdnCBkMfuluGgGvYBeODYHYRCgEJYdFSVIgtog8WH2x96e/3O+fee2bmTibRGHX8fcV77znnd87cHSef/f05NyNqWCwWq8Ik+C1gsVgMNhaLxWKwsVgsVqWDLZypYrEqX5loO/Pl3QGbEW0SLFblqykapU98HWvb9RrAlmngjzzr3SBbhrjGb8T2q277wVbF7zrrbVfL2IbMqhhsDDYW661QW8P4HdCDi+MMNgYbg41VGWp91PiHO1JflvPbGGyVCjbbfo1g408Ua4t0PP28O03J4Wf3788S2K6jLhYaJpMMtteh9oztZFNGSwDYmnO50oDat68peKC5LmdZObsZGBbENcuyGWyst0SNmWwmHNDf8uAeaM/yyWjTs85OANt1pXNfFZpGoyXBloor2Vw+22K1VJtSdnsR2JpzVnwdsBnBZIutWqTVmG0FcS0eLyKbBrbko87ORww21puhlLXm5Kxce5G71j0+fqn7j6eW73aSZi9Kqp07d1F0TOfbrq2VBptD+5wabAbbVqsKmOZks3j8WQHYkGvNpcHWFEy2GHhkkZqaiI1wC+Jac3MR2TSwPbo/O3tfJ9vNRCJxZsvB1vVFaAPWg98eguPogNse+cexTb/iZub0TwT3H/2wJ++2Pu4JvlNNuw4O5LVHJ0T/54eOPh7gj/xmuLZajV5bbi1ZCDYxhnWC8K1OF2znpMaPPBkauqCbRiwrwmDbbkUBaHvhTQ0D2lL5YCvDtRJka161YvLKDACbTUsWkU0DW2JWiNlOv73750KcuBt6ZWDrXUB4liDnaB8y428fbRBS0x/UvhTYCmEUBLb0ROk7LbGWOxvAJvL/e1hl4lCrWmZrVgOSJZeWvvvm1t18sF3/8wXg2lCHbmfncvaGwNbkxONmI55jOISXht/T5EhbtPJDV0MO2w0Ndko2DRnbQr+h7GJOFK4MfJmUP4VMYtIYVsarVOX8y7U5ptkqQ1IgW1gHW1muBZOtzmVWkMdmqyULyaaDzTv42ph7tfVgO3oYEZDuE9sEtiK3a8Ngk3fKYNvqcMYNIlNrQcPj39y6dVcH2/WxLuTa0JBHxkgkY0WjVnUk0lgObI3oWcQAQAQ2Q6LJACw1UU9MYYdGm5yUBrZUXAObd8SlaOEYgsuglmsjX0ua0S0gRr1FK0D7TDOjLsPupQTbBrgWSLa4FfG5ZgVzrYhsPtg6E6TOvLs8cbkWSJRIzNSK3eZOauLf3jPSmUM2IZrwL5otSFwRu3oLAlkfbIvLifM7KdDtgznnd3bMfAavUE+x70z96IQbGe46CFjYMTk5eYUgtTIFfStXuuYWD0zCcfL7Y6Jrrm9ucjIkjbrmbuy/Vj8/iR0wMjn5LwQbtJ9K6E3vn5ycooHvsf/KCgzMY5dCaNo0zQFgUdgxT3/kN3uISv2nT2KbSNVPI6OmSQMT0meDw9HHJs5EsOHl54cGHTymKRSFXpw3IY0nGF3rK+sAekCi2vKT0v5w+6+X7+pgu3N895DUp3I8hz8DTjLp4Fkl6kqCLYXeFV5J/ywLqMEu2Yo12IYGNmmsKGWYTgDYJKYazZgCWEq3odeVfiKBDc0Ewa9CFDPNiO+82RrY4pamXGHZQNO+/LGAvJpWD7V8M51sPtgSSlosuky4OfETgNGZQrABx/LAhiYINBdsvcjC5VAQ2GDkJizseWwdCMSbC6IDOm8T2KTTg0TZQfiaQrDtuFaPp665p7UjB6B75QqMwHn698fIY+uaA4Ouw/Vi/lo9ThErMAjXwDDiGpiN/LNrDho7AHXzgL8VoBpek2e163+HRBpzYQihCa/5YQ/BDHiEHhte9wO8Bh/izd0+RHeKl+CMHX2MdCSEiX5k24D02DywkceGxgWJO1aAx5ZDnysSEVWrfnZtXKHt0o9PLeeB7cuWC4prQ7+VJsmcpfyGKiuXXN9jk9RBzpB/ZofNRs+Fgh7DaSrhsTXYsVQA2CSlsFv6ZDG0VDZqOg3IA82TzKwUsDV6/3synVJgi28J2OKmDjYzvjGwCT/HBhAqAFvvws08sGG36FhwwSYDTmJXUChKi3hgI3xeru2YqS0qHZCbBkgjooXwCk8INe8abSTYQl5cSqGpmiNG3q8VaiUZs2LvvAIcxatu6QDxRD6ZFzpiE8ikTnhWkSbiTd2pGqRJvgH5cMVgc0nIWldhS/10rGlZsrGlB93j491L9/bkg+0r0dM2rcDm1UVty9ZO64HNhw3wpdE0jDywxV2uqRyb2wQrmEFgc1NrHtikAGzk3REClY1cQ64iwaaMKwZse01zr7qsyffYIFjMvUwoiks4dTWlqJfPvzJgk+hKYJCZDzY45oOtgybP1PfSOYTWClkbA9tupxbWOL9TuJEhZa8krIBGyB9g0UpIds1PaWCb18GGUenTWvTukFkjB6BJoafCHg0g5BBs0z+tl2Cj6itGiqd9sPlN4BGST4HNy5uZ7/WoO033YdScluHzAKJr10GYHQg2bI5ygbSscjJ+tK1GrXOMtrDdKwDbRTEw1SeeFIBNZC3w1JJWtmzxIM9jS6WEUeCxuR6ICkUV2QzTcAwR6LF5LkuQx+YTzHfbKkmtpmkrz7raNKvzigflybZu8QBDT3vrwIbsKfTYrgKdCjy2P9V7JPQ8to5NeWzoIf5lp5dzJ1CQnwUAQv5Mf/DJ+7UBYNM9NgSX67FB8Nn1H69+oHlsyEcdbAQcN6BUYNOawCREUb7HJmjvh7zTwW//C44b+WFAOMW2Eh4bHD45zDWEsmpfW01VZ9astfy0+tiDpXv3Hozebr70C7XfY/Z4W9/U1NTAEUm2Qb8muiYglNU8vtI5NjfvJfNrhsqxIY0ox6ayahJKLrYovxYINmlHYW1Ajo0WS2k5NkO4x8qQY5qSKoZjOs062MqTrcx2j5hltb482DpCFIoiiLq+KAAbZcWKcmwa2NbLsRWBLRGi6d078UVw25dXOtBzbMCj30yJArABxzCg9MCGvJrHJJyWY6OaA62k59g0sEm3C50y32PLa76HobGbY0tTji3dQ4WFCVkH/RWsoOXY0AybQWATo3Yfc6u8klVr1qrdmLLsgMGW50sHXbC1/X14anh4uKeLwOZvZMtl8VGbbK482LSqKIaEhqqKGlSvjKn8fpHHRsFnqlRVlOxicSqNFlVFZRbOr4pW0m46iD/BZ4u2GrhPV7mn/gbd9cm2/gbdMPx7xmo2DbaiquiJuxhTIncS528tYClBaaYWqUVgc7sSZ+R4KL8qGhLrgA0mhOBFsCoqC6odNGNUhWpqBwaGllNq68YOL6b0wHZjPwWaYgWrophPg9jzMlAOz4sEQ6qqUk6O6qVYFcV6gQY2iVAsZN7wPTa9SchCA1kVTZsQharSqPTe0pRwk6VQyqKByemTVGnVqqLANHMCMcmlg03ILiLbpRYx1iLanymw9Q1L/TAIXHvig9GyVquqVi0rWRZslD3Dttyx5iXKDAUz6XipHJsbZxq0+SwQbNo+tio5oXgfmwe2CtvHlrRNX5m2ArAR2Tb/SFXUe6SqZvNg27AwG1ao3vJPKJR+pErPxKmcvQjY+OomyDR59YKXUtlcfskq5gttTOPSwWbJFi10156nR7/zHqlywXa1YXpo6Hda+SHbDhFt1n/4YPsfgq+4BFpZNSDXHEc+Ktrq/exrD8HH4y/0EHzcWjXrApw9vdL6poPNKx0UaORAIca2Bmxlc/klt52lXyCo5GerNqtoUSCaXtpzavnkMwW2s0pXxWdPtFnqAfpwlMG2bWpBrtk1oj1cvXefv+/wFf7aIsfnmv2m/XaPQrCV0IrcS7v1YCvnYZlb6WKNmpxh2wIdwZxUaz7Yzi6KT9ebw2B79T/kyLVkcTf/okkWa+OKINgWkWkz8Ofs2R/EmwW2d05Z4FpAGYTBxmJtQm2R+wC2GdDX8Gf4r4LB9npl2HUtgsHGYr2kGp4h2L5Gti22CQbbGxqh8tfvsVib1MNf/ujfVxcflv0g89fvvUtgC+/lt531Lkh9YTJ/e/Fr+cbkbQdbjZGpYrEqX5loew3rdUnwW8BisRhsLBaLxWBjsVgsBhuLxWK9HNiqWSwWq8K0kS2JXLlnsd7mTcUV/Grvwo2yWCwGG4ONxWKwMdhYLBaDjcHGYrEYbPy2sP7P3vmFtJXlcfw0vdbGf0TRfdBr0preXLIJDYaMSFBhHuKW7ku6LRJGxRknSho66WBX0P5znzrTpkvptN15WdkZRsXCYMdx6JKWwayFTjHjUgqifXAXxIfptEyhDzu7sLPs73fOuTeJWpNY22o935h7b37n3F/iNfn4+53zOyokJMAmXqiQkNDmBdv8bML4qpWYnRdgExLaJmBzOu1UZiqfD6tYFcULUkDPq3Nl/bDn7t14nhOUAy9mja9DswJsQkLbBGz2rMCmgYw9WA42O4DNngltqbwwvh4JsAkJbRew2TWgMZzZQFarA2QF2bhceGOCI/yysY5Wl8vr9fmcSDY7cQqwCQkJbXKw2dLBxuFmY3DDfjYdbGZ7pmxUgE1ISOjVgY1BjSKLIs1iqampqqoBqaoF5bA4mDCG44cO2qLWqA6Hzeb10nE2u1NEbEJCQlsEbJxsVrzhRgebCmTjYOMxmwCbkJDQJgCb2bx7t9ebDjW3u77eDZLlRlBNY00NwxyCTqVCexVVDaDN5fL5IGIzC7AJCQltdrDJDGxVNVUcbBYOtka8UbC5U8G2bSO2Y9f/Brp+7MV/JJ6MhTCJ0+KNKySUBdh8PkxENbCpKkObLFdVNfJYjQmxxnpQtGlWC0tGFcXns9uxLk6rjLO/aWBTQ7IV94qM/1LPqm+tViTb9WOKCn3gt4HK+0M/lJUa9f/Cp1IfJGminfg52RT4ecQ7V0hovWCrWgY2NQ1sSbKtBButjDObswZbwI4b72YHmzUsgXYgiSSJbWsJmZTCJD+uHrsOXAuGCaGd4uzfv8sSVT431jI30hDd06ZWRTsKsyfJZkHG4ay+i9JfS9InnRv+nnn3vnTyn2Uv7S159G6d9GeMST//6/6xoo3xeUUaFJ/17Qe25OSBzcanBNTlY2rsISJMgx8TnVhghSE2l0tRzGa2kgFhCdrMYKtt1VWbFdiUOMPUkAY2MiTFlXxJUkm+BGQ7RoKSBjZJsq4EmyTJ7CzWyEyTSjrYjBsIthL/reHoBr9lrgTbfZ9PTThf0jvySP8XvbvPDgT8C5/8rtG7Mc9y9VrrJaf4sG97sKlpYFN1sKnpYGvceLDNQY41amweNRqjo8aAk9jb6cdyNMqZd4e+3EfQYm43RucjxNyGJvvMU0K8v9DW0QR1Mkd73vH/4/lg8ym6zFmBrRYDNCWMIONgA9TtiGMIB3QLKkgsCrYwUSYBZoTHZUgzagzSUA35uENrkePYkRNPvzBLhDTg5nACEQYHzBLrNMZITmAjOwcKzt09fvJ7Ug7ofDAdIYbh6MV7klRddrZOkiqKKwsJKS/EXekUt63ttLjyPGwvDhTgYSExjUSO9h8Pfk8MUh8hHfcqdu6FJ9pTcOBu3Wc/RAz7isjOpqLyClJ8bV8RPjIdL1nbv2Ef/Cz94xXdAwF41DEWhW/h98yN/+ypFT6ZLcOF6H7496Yo4See+BIvh38cXmYJXB3y9r3blfh7pYR7hN2VMd5LaIuDLZmM8uo0rpSyDjUVbAxt7JFWzGuBYyzUZf5wOgKIkS3YqMlrnBk0ztkfcbDF2mYQaNqdow1QNUd+nCmw/xK1v5WIjFJ2BextMXYIpzMn9L4m2HJORcNSELmEARgHG7KOhlwANik4JOlgg81KsBEGNojuINDTWnZgA5wcDufpFyZGBmfJ7BKJzTckentjCTKIFs9sjHTmCDZ/y3B04Tw5+jAAn1dy5r0Agb2husxU/eHABWJKAZv/py5uy+R0iTMTwQYIKK78lefiQMBwuSnqH99fgazAu8tZOtWQhJAp2IRg675/KgPYTNURuv10+EHdyfYD/YN4zNx0jDRfHT+f7pPZMlyIGxP/6m/TwFbsJW+PNRdXlsD3AC+09NmpQsIuA/NYXnHi4WnCeglAvIlgc2hludmBzWGxrQI2pTW3iA2ivUeAsVjz6EyB0+nUwIYnt2lgC9gTuMeGAAvKEIVwiH5/5E4Y2GgM9xywHRrSdShLsPFAKwk2YJUUIgxsWj4Zlibzd0hS3jKwxcNBZoxLeQx7tCVfmuSpaL5+YZZ6gV0NFGzGw4fhRceW5tESI55ekusY25EpLR6BMKWv9GYDMX0DsPjPw0Aa2DrGHnNbDmD7GhDQjRioLDRM/zzY/fCBBrZzd7u66koM+NQYBGHMBGB7Z/x2ZZZgu7Wnk1wZLgImVbadaHrq/7SpaAG9VaT7ZLa1XR4Aqt2Y8PATO77s6tpXVPreaQa2hUvlOtiox/LLz+Alsl4CEFsebIg2DWxaakkXglqTEwqpIGNgw0e4BIsVibCiD5baYvmIy+VVgnk5gG2mbBR5NAeZZmR0zv+W8UIyYptp9q4CtoI0sMHhHX8nc6JHbOhnVbApLl1KlmCLK1/5QpiQ6mDLZwewy5OkoXByjC1IloGNj86RPCkO90mtZYhFbLUym26lFwbCtVkyuEQ8p40cbGjxQNyW8OSYihJyZIoOnCPYILN7/G0zKT8P4ChruZeait7uXzJwWw6p6J+AARrYqt/94lafSQPbwkTZkf4SLbq6NP4R7AzDj0f+V5llKmqAtBn8AGsGLhRDMv1fgNg3Ttoh1SezrS1MvSE7Zid+MNVGLjYVdTdFKdj+PVakg415LP/jtY/gotFeAhBbH2y+lWCz0pWgLwS2NK5lBptndOYp8MiIqSgA6U5ZKthGNbDd0VPRWGoq6mUY6+ROMoIt51QU8s6uxcV4yhhbKtjIUFDhYIuHw7XKcrBN5sfp/MAkC+3yWEuttNoYG4Cr17jEDg/j+BqzQB6a8OQKNrIwPU/+4KFgO/Ds4z5yBoM2yEZHIikRW+uE08BtWU8ewMmQtV291gepaKeh+v1n+wM62MonnB17dbC1jkQQbJfDgeJMYNMmD87cbCemb5v9460TtLgFU9GBADk3n+6T2dZ2uVD9F+X9fp7DfnCzzf/TviLThIeC7eNBooONeSyvKH1WUsp6CUBscbAxtLlcVisCKnWSgCENS3GxVJfBTbNpaHM4cB2CLKuq1YrDaimpaF5ukwcB+PiaOdhmmon96aqpqHGOTR74ynDyAA1pkwfcycanokpQ+s3iYhATUllLHlPARvThtXDqWckxtnxMW0M8Zw1qs6JBssqsaCxmNCZitBo3AQcxZjGiNWewHbhbJ400U7CRlu8CpTe/KAOwfQiBFoKNPnV75Z6nxMBtmdzq5R6IgytjvXzyoLrsxnREB9uJ+5/98LMOtu8acIfzCxnBRs7xco+O+2x3j1VqwPnkt6ekYGe6T2ZbG5U0ZG2Z5iN1LXUnnzTdOtmAl2fnXqCmDjbmES4U4Jr2EmDb8hEbjrKZV4LN8aJgy3LyYF2Kel+s3MNr0+XNCmzEClxbXPyarBNsEKxN8lYZrbS0bejl1bGtopbpyGrZZcnmfYfivKiQ0LrAxsppKdhqanC9AcINcYX4QmTJMltixeCm2TS0WSyNjW53KCTLDofXu55yj9cCtpxTUfLVkyeLi0+e+LQVBVZt8YG2U2WVb5KSZUVrwV58LA13sj6u9qpWHhzpLyRbC2xXx/tEBZrQOsHmZzHb6mCTAWLuVcDm3n5geyV6iWtFTZlLvjaZDNJIr/iUCq07YgO0+e0ul8NRVYUAY2jDhVWyfPBgfX0ItGtXfT2DG8ZvaGUxm8OBMAyFenrcblV1ud7otaJCQkJbZ4zNTym0cWDLda2oAJuQkNAGg83p9FO5XBaLLCPAGNpwITwirUdXaFcoxDCHYmizWBCGPT2HDoVCjY02W5a8EGATEhJ6mWDzYyr6XLD1cLDlwX0XBZtGtoMCbEJCQps2YvP7nXDzK4rVqqps8gDLOvjkAZ06cLM/p0v/kBGbE03OimKxB5s8sFgwFRVgExIS2jQRW0awuXWwNQqwCQkJbfKI7f/snW9oVecZwM/0lCtaSxu7fShpjWxzS73gDNFJWeGWsNIbmpPL1dtroN6GYpqESBIy7uZ/DMq1ayHbNKW1KpgPglphdBs2DLoPwmqwwkrBEgQpfht+WP1WKPuw53nf99w/8do6G73m9fdDkpN73vOeP+b8eJ73PU+OzmNmMr92tQfVlaLlV7ZU/YmiuDA+/mNF8SO6K1euXr1kCWIDgAciYpOALRnMEZv5g7rlsqpasa38/mK70hCvXUFsAA9LxBbYV7Bo8br+8SJTDPVT/dOT+gLltTU8t/Y5gyyYdkuW6Db2VTBr1y5Z8swzd+iL2Suf3netfXplFrEBPCxiaxW3BZk7EFu11r6n2B78ywIAC1psSRO24QvEBuCP2DQXxReIzRsaO/MED90djNgAsQFiQ2yA2ACx3RE/AADwjCABAOAZiA0AEBsAAGIDAEBsAACIDQAAsQEAYgMAQGwAAIgNAACxAQAgNgBAbAAAiO2uyUaJbFvPw3jpU4VEKs1vIMCDIrZ8c3NzNF9HIJ0V5u10uszLq++bLlJmd3d5+N1DzW0dd7vnYhAE23v5/QWY34gtHz2YJ9Td2XE/d9eoaLM4efV08qWb/AIDzKvYxjs7NJeKNEiSwEOWE13p+IfImK+7syfR1dYhH+sqCVCac6bBdGdP91BOthgfSifyOVlTcJlZpPGbqEIDr5zGQ5GmqgntKKWBmP08n9flbHR7sY0PmRYDJiYyXab0ix5Cc0F7Kx9sjwu8Iu0u1dajjaftLrMmGNOuIj1Kexh1xWY6koMfHyrY61B75l3xOdWcuWujfZgd6S5kTdUFsIc0PVQvPC5O3jzYVOpYPxtkpnoSeyR+y/ReTgbB1LR5qWLpRtCbeD0odXzZJD8NXk5OuY3MhtJkf278RjLIrDZ/bPTqbKmDWwEQm+aizXKDpsQecm92RU5s8Q9in2yziq27s9Pd3uND8lnbtN7J3Z3TnUaFqQEjtrwTmxtxkk+69HPpKJEvlMVW6DKrdVVaxJD7NrG5FvZo1BhdIouUcUk2isWWNZ8l7Eoz1rexs0cbx7s0SyLw7HeIzXWUL+QLibLYKmduV2fnnrlr47qJYrFVXQB3SOrpXL1UNNP7/vDkytPBaGLTZLQp03twjX4dy8+Woke2Br0H20VsB9un8u1zxFbMrDmdnLqcLP1szctjrwejY9OIDRCbi9gk8tBIQm9ekYkZbUrHP4iwUgNqkPwjcntr4JE20VLbQNoOLpmbOBtZgaXN/Wx6M8rMmcglZ7vUcEZiGNmdjX2a01YBdkWurtjG1RfSwgiqIzZG1gQ/Lm6T3sx4XJRwOslG450vO7HZXWbNag3dTCDZnL6d2FxH3UORG3VL15y5Xd0198xdGxex2V00F6ovgDsku9Gtqeia9uXPi7AOtg+OF0sdezK9W9vFdr2JbtXUiWC0OCkLl5O9XzYNaiwnQZraMJj8pqnU8/5w6XTGDNGdMFvoiB0TGYDYrL/0rnYuM5FK/MMjckNOi9hScmt2aDKn93qHjbe0hYQ2idSYcVV+zG6cML1pEqsxnP6zAZwLn0QgLiAsi02tGv1/YtOIzXztErOUN3ZiMxFdJWKb1hAzcv80YVbJ1Beb7ah7SE/ARWxVZ25X33Lmro1ul6tEbNUXwB1S/YhNg6/MGiu294cHE3syV5tKuRNlsWVWZ0bFd69nrNimxiQ5LU5GY8W6YitFW9sHuRvgoRfb+JCmn11R/VQ0JzGb5nxyb9tkS1PRtPGAScg+kDtVwzq11JDN32xvKR2LMzmkRHJ2AMqKTYRgk7p8dSp6G7F9aypaFls2DoRsKrpRU8NqsXWawcJ8+jvF5joyKo7FVnXmdvUtZ15u0+12lHPpePkCuEPSrgv1I7ZvTCo6dTo5asU2UKxEbMFgT7H0/Ozym05sm1RsVanoCU1F91XElkRs8JCLLW8fqdCxIgmk6kwe5PTmjHRSoHx7m8mDqDKEXkjZcE9nV1Px5IEmi20DY+rAvJk8sCPoEujY5yrkmw7L2amB26ei8eTBRjt5kDOJbmXyQBPSDpfYGmOYyYPmXKJGbDrfsHEgJR24VLTwbZMHcmzpqsmDmjO3+5l75pU2ZkdObN1VF8Ae0nTdZ2vc4x5m8mB9svQLEVvvniDz4/ay2Cb3JYql2cxUIk5Fp3pqJg+6byS1TTkVLe3jbgBS0ftLrD7r1dydbZSN+P8FQGyIDQAQW2NAbADgndgAABAbACA2AADEBgCA2AAAEBsAAGIDAMQGAIDYAAAQGwAAYgMAQGwwX1xfIfzRcf369Z9zSWChiQ1gLq39K2rYziUBgAXP/hqvneWCAIAHTBCwAYB3HK147T2uBgB4wfbKMNuxVi4HAHjBsdhrYrizJKMA4AVnq4fZ3iNqAwAPcM98xNMIE6gNABY+5pmP/tZjbrStf4JLAgALHg3WDsj3A7HaDnBNAGChc2ZFv1NcrLZjXBQAWNhsL8dore+5obajqA0AFjb7K4sVte3nugCAN/Fb/ADIGdQGAP6pjSd2AcCj3PQMagMA/9R2lGIEAPCOY0cpRgAA/9RGMQIA+AfFCADgIROoDQC8o3WCYgQA8E9tFCMAgH9QjAAAXquNJ3YBwBsoRgAAn9VGMQIA+MMx6qwAwF+19VNnBQD+QDECAKA2AIAFQGtcZ0UxAgB4pDZe+gIAPqttPxcDAHyBOisA8FFtFCMAgH9QZwUAPqqNYgQA8A9e+gIAHnKAl74AgMdqoxgBAPyBl74AgH/w0hcA8FFtFCMAgH9QjAAAXquNJ3YBwBsoRgAAH9VGMQIAQAbcGQAAIABJREFU+AcvfQEAj9VGMQIAeATFCADgIRQjAIB/8NIXAPBRbbz0BQA8VBvFCADgHxQjAICHUIwAAF6rjSd2AcAbKEYAAI/V1s9LXwDAH3jpCwD4rDaKEQDAH8p1VjyxCwDeQDECAHittv1cDADwBV76AgA+q41iBICGMflh+Nd2+f7azMUtDT+Y5U+FlqebFvAlpc4KoOE4o12zfkNs86I2ihEAGi6THUGw93x44sE4nifDH3pwVct1VhQjADSEIyOn3pYvH78YPB6Gshi8tDMUuSwKW5YG8pEET4Mf7Q5PHt8jeeu+3ZV46kkXXS0LMvs+C3f9pRjINk+Pnhs5vFWXXMPecyNm0yee1Q9Mq8yH8crBf43o0mP1xFbZsOV3n2zY9aN214Uc1eAnG8LD65MuwNNWsmS3kjbSW0kO+PB629/iVXoe5mzK52Ea7PplUVovq2o0r1CMANBINu8MX518J/y9WiwMX9XkdI7YFq/a1bc7bPkq+LOYad05J7ZrfX0bwl19fZeDa0ZPLXtkm5MbZElyWxHbtr6+fze9YlZdfEyNc3zd57tD8adYaJv093SThInH//v5TF2xVW+ofcrxyZL0eXzTG/8wYtyRlI7+tO63n4WnvqoV2+YL4bYvNoSH5oqtfB7SQLg0fC/FRjECQEN5ZeTS6KqWt9Ri22YuDQfXLr5ZK7bMc1Z/oo9Dap54BMzp5I1V8rGEeX9ILjL+uVDeWg2yo33yn2WHvDAiH2/eefJXpuNF4U8eFafUE1vNhpeGM/8JTz0aa+haeKoYvDtzcYvdv+z+sVqxvaKB55EZcWit2OLzkAYtW4LJ08G9FRsvfQFoZMh24eQXYiW12KWvL27Ze/7jr42ayuP4gx+9qfHTMp1BbbpVbOKnt3XjUy8u0rBNxKPOMqb4zSqdmRCdvWUd8rhGbJJcLjVie23m4tbbiK1mw0MaRbYsdRp66SmNLp84Hx6y+393puUtm5RKDmzE9mH4t2Sw91nrqsWmpyM2FbXnYRsELj/W5PQeiS1onaAYAaBBSAoqMZQJz/4e7jgS7njSik0SP80YJXo6nIrOiRBemKmZs3Rie1wDL9Xbo5Uoz4nNflNt2AGyUEe4Fq+S9tpo+TvWnXXEVrPhsuql/7F3NSFyHFe46OnT9EzTM/TM7Cxs2IU9KEIHidV6L0Y4iwiB3YCIgw5aL46sJCYQaResSMraJiByUAIJSPnZiw7KwSfvQRYhAlsRxihW8EHxOZccHRLwLTiBHPLe915V18z+IEs7K+3mfdij2ZmuqlfV1d98VV1ftcosKjvTm6jEZxiUbqykrzCx+XurqBPGpVQNyi/UI9Z3Ny9tpA9fGxWxmRnBYHhmoMEcjUDBSP+Z+uSLWy+WA0PRr62Q5qEhXMY3Gtb+u7GTYmN1tJ1iu3ns2EZ6s0HqaeKCjHFJfN3ceo5tIOHPtlds148d+8vKjbcQyan30o4qNvqY8DIyfGNjZe3OXYqnqkek2DJ8MjpiMzOCwfAs8MMjv/48lbUeTDbvPbz2yYVhYqMB5qtTxAHf4Em2zXNs96M5titH3v5DemW7Oba3aVxJ/HNFJ+9+9ed3GhiK/u7Y8g5zbO80Tv2JxrDbzLFRyZ1BYjtNKei4r0S1TEBsvh4Fz7Gd+uuFQWL7zrs/GjW12Ypdg2HPxqGpLs7FGHKF9NAgsRFTrX1v5QUQwh+/vpnYXFHdFU0/lBUZSmxEXfFd0Uufpg//PZU+fDFk/IrMsZUk9waIbSDhh7KqxBNb66OBu6IbKW5r8FD0Vg5iI/5do1F0vMqX46nqQe8I0w0dik7WdaQ7shV0ZkYwGPYWp19Iv/ut484T27c/mvz5ELG5Vz9NbywnK9kb91nZbSY2XnO2dudlDEofbaQ3XnOB2NwqL0f7h1/HduvmW9+/v/bBEcn4cx4Bg9hOr/z9+CCxxQm/+fHK2gfHq3uYP/j4zfTGS8fdwBwbT+DpzQPX7L1JH//0yCCxhXo4rIRb+9vxgZsHzd+sjXCNspkRDIb9ikBnu4hAZ/sd9tAXg8GI7cARW/TQF1v7YTAYsWUHpoHUjPC6dRWDwYjtADURqM2IzWAwHCh89Zev21DUYDAYDAaDwWAwGAwGg8FgMBgMBoPBYDAYDAaDwWAwGAwGg8FgMBgMBoPBYDAYDAaDwWAwGAwGg8FgMBgMBoPBYDAYDAaD4XFQm3ULdWsGg+H/HUX6FA/U5CfY5c9TbZrjafxA0adCmY7uUaMGg2Gk6NVr3SemkbHGAWb83DqHwbBPQdzExMa6jZ87PN2Qp8NPzI/z49dL/VgfqHK04WrdBI9Rh5xJ7kzx4+P5W7BjggfBSwJ+3xHm6/FHk/Ve3SXT5/kpxctKiEmH+aNGmaxOpSmeCU8vdByRSpJx4la/TV/j4fLp7/m5yFmvHrTZZL30qToQWDknKUiy4RHKmQTSu+aPafo60d+UHyJvHRb+4koUGgBKbP3rx/RaUEXoODQMyVOfhD5DShV1qMfyYluDLibWuY2ucpNQBVAgl50n4WOuwKFr3FjR8ScaFHjGVcubi+1kYrXLfxcaKbdUVw6QxlWxXUg7owCcOkrG1UFsqIqE77Ql0IDIS8KtnWggI243pNOkSCV1TkUGc0Um2pKLnBWcuqia/tjSV7bh32VyyvhfKk1Lf7rhgsGww6RUF5zEuq026yUYERhd0c1DzEX6riI2x7NYfCmXuL7ptSK2jHOSBPS+OXZGia3I8E+rf7fhqmL431Z/njMHueaUK300SGz8dW3u3AynaJ10zhObZslMK7F0pLzabxfbeqgEUuauNdOoaoI0VAJdixRj72JMbJKJlHgWtSzu9duUnN/WuiFJcokCvJRLyb4entgQwUJdmoSS9PStNl0tEBsXMx8df2kW/zOFLC+udxDmg1lUMxCbfIDGbYhk5lNH/1LlOE49RUkmsfF7DR+haktExHZ1rh1p7ySjg7RB5bRSBZy2Or0wgXEu0kbh1Gk1/bFyHn0/4ZiQmfYk6g6e2A646Dc8O1A3ZR3Aus0rNvREEEHOr/JOh63oqQtgHr54+HLLIB8iYpMEidcpLNX0uuhdHhNiG09lbo6zwNUgxFakcrgSGx81cY6+pssPbMBsVerPP7IsOWKJBWkvE7Wd77cjDkQdhC31b6QBy7a5eK0ahyuKZ/I2SuRsanNt0E8XV26RhSTJvf782D9zKVnrAe2VNTWCBcgZhF+q9GEpox9PKykRHUbHv0RhPpqtpgrpt6YL6ZVpePqBRAu9CMmHU0f6iWNlYmP1m0lsHLqGj/rT0RCQ0MkQtRwKMtJmEOWqJ9ehzoWeLaEu5HI+tFGopnxbhGas+37ikuiU0Q/KTMOXHhVsMOwmuMOzaJtr06tcnDsoNuqh12PFRsnkp12ZZ0ixORBZknnFdhFDRVVsYMLm4t1Gc0CxSf/fWbHhKvWKrdVf94qNyeJivdUfUmyZo9HWgGJr9Sk/ZqnPTnrODootSKlDqGXvtldsdHxIkuQLj2aToNhQDx5XLWU+ApVmnBwFvp9zI/uPuVAacNIwdz46fja5d7IGYutdXlylU0JSTuglV8XmP0DjPupyqDh1j6nYfEvUupViOz/DcxHhDGc8+A6KDXXmn5ayIjbkMqTYQjXlWDmPQbFRdJFio7r70qOCDYbd5DWe8UrTX0yxbqOBZUVs/GOaBVmUCY9U46lofkd+kCPFJgkSP1M33dA5tlIGKLFiQ8f3EzXc41nWlIgp9XNsFKPMsXUGFFuYY8uqWKi8zFXEpnWoZpZKP8f22WEcl5BcIZ2YVXNsCEBKpLCmG3wVz/E03/SZcQQlSRLWHUlezRHppcwyUyJQadbRyaeM/rg+N6jYZI4tOn6WeWqWzwrPsdVOXP1JnceGfLgSGz5QDcSNO7n0CKfOz7G5itgkNhkDT8VzbFBJ0Rxb6+xlzqju59gKnbzj3yupM6VYihQbcglthOnRThiKyrGFl6dc2jIzOLoPtz+0JyYaocmpYLsMDaMQbM49zm3RoyOZCtmL3+tefVeqBs5Pst2rx97PLvXqTxLicJ17T3fKODubWDM8L8Q2EhR7cU+stzvcuROxPVE9jNgMBoPBYDAYDAaDwWAwGAwHAa2TLjHnlLW2wbBn4FsaI59lLnVJ8vOLIv0ytv7nbleCfdbaBsOBILbnHtstMNka1l4Gg/6IpvfgS8dyUVmaKdYbWYKJS0uc4r1662xdzM+lerDDEtVoYSsvpVWfIRZ4dsRwjgW1MGm3nRqhl6bSCV683uqvp7ICNo9MNkpsVabbmevdZvc9XjtRDVwhNnQxVwa7O3z5DbFn8wJgToCXyoCPRcbqvReXgpq4m+NiIX+fvv5kBtsDoNiJc4f98mOxmHu/fZlJCOpcE7uZxIhXTS7lqfG8OfYFW5T8wufJetyMGmTk55ddCSqzeUcWNvtm8lWToCfWkQaWqPamc87mJ//Xki7YdbIWWIxV0hmCOz40TdyHgsXVu0kTk2yGPREEWIDFZgB4ZHApNaRTuuCDVKd47/ZMQw9T7ycudK8SenJFsIEnvghkkRxcVbxq7qg/uIAhq2BLojiGkCKyufPXPgxkurW5HkvxYi8XLNdIENVAOEkiArF5vz18+d7jRf9pLSo7FzOGD0qITU3cxYNZtZCzAy2HU52LpSjEF8XZisUc38GV5Kq9BppjjRAeCg7J4ZqQItl3VZs712+LoXewGZVjNH+Y87ErQTCbU3vOqLdCjot87+JMpzSyB8Kmc642z0w7STDFe2LTzpCEvQjcQJfYmtiktQ2Gkc/g5J7YpL9CMJXYcAaOICd2aBxWTopNUy3lMDMHhcVObaQI+xd1ArHBGC2ZKrGJEVpNPWfkAhCbeGSLjsJApluY6zXTTe77zFuJpAZwkCP/eU9s3m8PO6snNr7S60ilBvzDaezkgundx84CTSzkXCe4JKGOsA+IJ7Zxvw1UDne5hBAptom2xIiCQ3L4XEUE4bRwgUUuPyhxM0qQ4jtXcz52JZB2gDtezOa+mbRqPmhJwx9mbuici+c+9ADfrh1V4XSeRGfKAaXunhB1Ccmvykds8tLaBsPeKTZYsle7ahMX8sK3wSneu3yoHik2b2b2diLso5F0vGJjX7zwRauvMsI571+StCca7MtOHsx6hSBe/Ghpuw9jULENmevdoGKDUECCUAPkjvznI8Xmgi/fE1uZCz0mnUqxueC9Z+t4iB12dFjIpU4LF3O3hWI7D7M99E6RaRV1rwEpU2Is8yHF1vLG8xJJWu8utjmEUONIsanvHGdJdiWQdkBjinL1zaRV80Frmu7AHihRi4W/eHSbR+eU1Zd2Bp+vbExQdYlhxQabvLa2wbAXc2y5DEWv6QzOku+UspWHE9u3TmnpvEuvLj/qPDEGG3Opv8+UAnNsopo8X8AYLZsy4opUI/QSpmj8gAY28dUTTDxhJiaEATWz2Vwfdnqs3PdNsVxrFNe74TJF/pjASnUmiHRHx0UkU060RThd71YGfDZ8n3TeOh5ihx0dFnJsFSRbaMgkWdsP7Z18j+rDXY4Q1nWvAdkJAKVpwT65lgfjuc5zFTC1q6TtDBCb+M71LBV+z82sBne8i+ZEdXeWKmhJI6b8oXPuNZr8tRTtdRDm2KQzYG5NNyaIu8QAsfndADp2d8Owx/jSPe5pPH+SVreSTfbXHqrb1LsYunup82S7BJkqc2GmbO+rPOouYTAcKGJrHd5nOw1uWe/a1Ejv9pV++0cjNoPBYDD8j73ze43juuL4MDsPZmd2mF1mV9LihV1QizGGLBGO+2BMEXpo0LYYXNoiszSJnoLRD1LbilzXAT/EKU0eEhP7JY0NRn5JaO00xGClwRQ3Nia4Jk+l/0BL89CnNm+h59edmbUkIqvJqrK/H9CinR/3nntm7nfO3L1nBgAAAAAAAAAAAAAAAAAAAICSvX1cXvtd+KI5z8nHWT43AADsGGHTt4/rqycLX9ybLLPsIAAA2DHCpm8f15eFL9qXTuDe/whhAwDsQGHTt49bxJZ/yZ5cA2EDAOw8YdO3j8vLwgtf5LGHJmw87AYAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHYQlSa/PbRdhicAAI8Nh/+2e7n9/d1/hScAAI8T6XjklTq3H1xe3ecHsXd+oVWzQK5VO/PL4OqJSvONtxeunuD3w49Hzz0I3jntpbT21GeVJm3q8eeLywunPuPCaPVbp1/9dOHU6r7DtPPvIllAVRy+HoSlTui93hmP4HMAwFCEbeXYu5cPkrD96pNbrFa7ZpfvXdp1fmH12T+1Jpt3fnjm7sulzup3dr3e+cfTyytROv6vp5p//MoJ2+TyHy5Nv/Izj2TryrGX5q/fO/Jc57fnFy48/dNFWUBVnF+4xcL24+VbEDYAwJCE7Zz3i05IwvbnlS9ZrSQOk1W/by81W/M/aLYWO/xq+PZp73xwUCK2FziuO9X4D6/iAC/W1V71I/4W8s66gMqZ++iDT0jYziXtzyFsAIChClv7+N2D6WaEjSK26yszzXuXkqDPq85pWSZsH7pynbDde3dlbi8J222SNggbAGB4t6J3XvCD4OV9BWGTW9F7X8mt6K95hMzTW9HfsLC9Pc7CdvNyn29FV/753e/Ne97P71459uyR6+3+Uz868ZOFC7tfWpQFaXAnrrKwBVfnIWwAgGEJ2wcPTvGPByuRVxC2w/bjwZvvy48HJGxe/uPBW325FV2VHw/+snD5Cgkb7/DOkVc/fYY+KyPPBFfmZUFKeinCRvEbhA0AMBxUtDZAf/wEAAAIGwAAQNgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAODJY7pc6SGF6/+bblSd2vzWpf10UOE0MET05QbhttSdBkF9vW7QeUR7En47w9dWtU2NfDzx5XnJj3CSIdsYDJuRbbqYJvE31MnCTbWxOoHnwAHwZAkbRUntcmXPa/xJMVyo35v8xtHqXvtXHhDpc5SV8vU6+4+Epbo39teJiWhtSLvTNlIe736U95Iiq/9e5mUSttG9CpmhBZUadIUPLXSrazWsXQmv0QBgNPKqYzVfA7XK6JdUAS9LWrWR19igVs2PK02u1AUKLGxjtaJFft6goK4tt7poHzajo/Gk2CdVlY5KebyACqfbZdqSymqpIWQc7TI+wxFwSO5qL5nLyLLSoUiqS/jNXxe1lXlhZoJsRnb69iDOkXL1+bL4jdePR+oo2U0cQe1xDUzFxbZQ/MYHSA0N8qPJ76Ro2XpylVbFTlbnXXTVxJ7bxg64GOipx9zxoDao88wyPbJ+bqkUoDXrsUFPA8MWtsqeslc6MKmfdBpWsv8kHPJDUh4+PTXs8ev0Zc7+k4hp5HjcjdYNnahw3lfKq+kOaSw7Ubelr7ogEzYqiDpocnu/hmKlBleYxOsKm2kyd1ixtXShV6OyaY/SgYv9PWWu1JmU5i+FVou4XGd9ZXRG7JvVuk6SaJ+Mp2lJI6uOd+MGJKG1IO33LtJ/ZKAZUmpIfaTaU2RrKANLsmdl9OyBmqtOvcStLBSmJvBmrGZjN0zYrk1Ezm/TZfOc7mYaNukayE1qFIStwd4yQ8kcO5o33qtV6E/Xj5StKnZyRZ1n1YjVuo074KEdcL+eHQ9qA1uZWZY1xVnKBSy580iKB2DIwsb9gfsWC8akyQZ9b9pFV6/843a+85hW0L7fcHeTfuiHiYvYdMzOxu1411hkRMrTLsIKxUXystKBm7EKGPc+LYi7qOoR9w6JPkI/sLBPY6CmvPM00RdjicxNzJD1c2MchvB3GQKSyKw+IN65RdwQUQEuOlapXNS6PiYXfJFFbFRZLC2WrsoGakfXYaMkpEISM67FDaqxsKngOms5LrLqRNi0lXlhagJvxnqzNKrClrbLmd9IPhLnKP7kaGh2bNY1MOWabGEmbGYomWNHs3cz9ld7FrGFrip2ckWdJ9UEegnQbeyA+675mY9Ctd3LLdMjq5/OxtCdV1o8ANsTsVHs47cGI7ZSY0SuyX44ELEV//P/PkUnM63eTMTWqlGEJUVqgKOXd751O1rWgvji7luf0ojNK9yKJk7KxrgPS/CXasR2nCKQWhp6dENHyhhToXvKA7fbNpa4NmKjyEJaPqt1xdP39/uxBGG28zWpigr2UhexjSz1FknExmrOkDURm3OZxDrFiE1bWShMTZCQiOKgigkbhztrIzbZTaKhaxKx5ZemxYZZulHE1pud6s70svValTi5os5z1Xie2yaP2CSAtIjNHfLBiE2O7GDElvTtPNLiARj2GJsOpOkYmwiYG1iTwag3G3zajmZjbPIzZD7GRqFG0mdpWG+MTe7JtLxsjE2KlCGpiMuqmxlSUFx6RW+wJOCy0bk80LNRK45CqPSj3LnM1pCXyRhbwmNs1P+5hFiHrNI8tjGLtHaNRlqTOsamdcXUeUkYQ+ncFYlapSobFmODq3t5jK10aFlfoCprXYNY2Fioj5vL6EMHy7g6FjZtZV6YmSCbpXW7MWZ/kFCY33iyRFIYY7OIVxporQuzMNiJknqWzVEP9WpJWHER23gkVc2Jk/vqPFdNK9umMMYmteqYXNuOlAmbNeKoGww1S6WA4rFBTwPbg4sVvkX8zc+5kK7wqL+cbvEX3k213AVwD+3mb2kaydrCCi2f2tJuW2FLTv5fjywAELYnUNi++d0gbAAAAAAAAAAAAAAADIDHBACwRb5+MJjnciK5eTt45McErNm9PZT84ATnB9h5woZfwnYmQ5tShtMDbOvV31LaNZt7UtKmeeqnm43pyaxXL+VJ5ZK5k12FfU2byhOxdW4mT2rNJqy6xG+X6/lQ7rZLIR9I7uayNQPf2yAZvDAdtNTgPKbny64pWVE8L5R2eWOC2nHBJb5/2LQptQHPitdpvrEWrDkYozqpVCe5Wvq2pHYPpN5LO2VuiS3OZtpKzkFg05jrOluVthGfiC/YwTK/grOefMlg0tbI0wdkbu+SlMm5qElf3EDWUB2cKDDYtrrMyrU8Udn1c3F3/qgBM09MtWkdyUmeyTsheV4JW8V5Be8XMuIsl51X120+sqWdyTTqrHEyhbrvZsroJOqs0qQ1KU8nyHPnOTUhe9QAAN+ysNk09ThLK+ckHE6OKR3S3HDLLO+ejLzuyZlCZrnkTA4kYmtH536epxhZ4ncubMXc7SyFvJjcrcLmMvDXTQbPc5E080o6rjYlKyq5vV8SgJK4kEal01/FWNpbEo8sGdNzwua5pEwRttKF3qwkEw2k3ku+VVHY5J9u9tAAl/8eaXr8aETqwdV3I+dzzhQNNVmprK1JxJssMxWXtKuZu2KNCJt6v9A2TdX36zrjX45LNyo+amA9YatLPbG2Qw48lz/lvK55bD7ppRZoSfGZsBUa5xL9c2FzlZLbJuXpBOo8Pb/YCWP6qAF0PDAUYeNnPVhaOadNT3Dip2Qe0kmq/b37BfWo7lwhs1yfXlNMxNanaHDHy5PCpadlSezF3G0VtkKCeZ7H7XKZvA2SwS3lOpB4xXVpEzYtSlLpTSm5SEt8V2FLNQSbGY0s6VuFLQ1cNnndCRunby9K+vdkIfVekyxTe0KRJV1pSOkitlh9IVtqpMLqTL5gj3HD0jDNhE1aw+Kjn1YmN1Pd4IRNvV9om6bq+62LXKLOTs6vI+7pBWpeEDthi1n2xCt0nOWilsQDwuby3e240hHtjEcaQmvEZo0TYWvqswgKx7iubpOnKUyc1fR/Ob/Ev2c7eOgnGJaw0RmepZWvjdgks7w70ztT7s4UMstdxOZ5Xp6IrUHHhhHbmtzt2UKCeSnL43ZdzNsgGTxLua6MUs/xw2LEpkVJKr3GaNP8hJ2HIza+q7y93yV9FyM2SdF3wsbp28WIzcw9UNOIzT0MRRvuHgQgcnVfFsmWAxFbEuvzAPRWVIVNWvNwxFar9G5EmdJkERs1pdA2DgjdrWgesRUeNZBFbBSAqbD5ErGJV0TVvOp7vdp/2Tu/0DiuK4xfduYh7OwOs8vsyl1YKoENQhQscGS9BJMYEVzcgqEhAckhxLIDeRAS1LZsySVgSkhooVSJmxc7pg8ShhbsNCUFxVVCMGkJJS1+DPgxBBxwodCWQB96z5975+5qZSuO/ljy93uQtZo7M/fe2T0+c3e+8/XM2GxLqbtijMsdJQrr4FzGphmoxmU6qVQkKDI2fn/VuYMo+Am2LLDdHEoKWbnKpul/ZNFgyxrbcMW+z4crgbLca9W9EJurdNwWlbcThXelEIF2u6/sT9oh7ubI5zOBnmJwL6aPbTSkzzHXJJLAJocSKT2v5/BHiYTv8mrMVQrnneSbuzCwsUSf1+v2jot8mwcSSO9vDaTGZ2xy20gDn3WFAEq6ltY/8Tm3dGtsPBf2YL8eDVcp+3SNTRT6xRpbnUNQy+VBsYrK4zQYm0r1BUkMabqLUgNFr/vLUvHDVQKgrFwOyhExDGxy5ege141CU9O9FcnY5M9dGZtLou1JZdrkotGxpuT9ZVwJyn44IIBtIvhKawtqh3doINfhE3KfL9xWyymzNRqXHrCGvQXa2fuOJqy7tBHHMx2WKrrCR2uiyKEAAtvmB7bv8tFdfShaH+rVrjb0oLxhmwNb9tBfHq7jOQueFQls/8WKFwAAAAAAAAAAAAAAAICtJhrdDiF0jofbAQCbx/Y4zcM9BIDHGHlylJTmp1nwwgJrkc+o+i9XhbY8HcH27M563DZ1tuudju1OpG2c6l2sx93xUhF801lvHFCPP3lsVMXvsl0exu3QW2ftuhepe32i76EbQhBPc6cASvlw3t1ONwRK/cOtsAdemF54qDvXZbvLZ+RPlciTy84Innqjnlt5YoYr0aFx6XDRBVbbf+28UWWGvYpfvelzp83KpCqUPmKrbu7chVXjpenVGxcuAAAgAElEQVTWMfETu1lDPeaD+SFFhm0nF4fqubnnl/WRYN9dX+Yg0wuVuieXe5YycOb1cpGdfJeqD9A1uy3uhkVVADlrm3V1SKrBpt4rNsU1UiXV2a0RUaDrs+ROoS05EIsUnfU4WbaL7XqXY7uKtEnEwyJ1sR437nhG5EN8VhaqshCcH0iVU8t25+1Z6K1JTcTnDwOb76FxQzDGS75F795QQXpWBLY+35L+Ga5on1wPgmGrh/qkc0Lm52ZZwJCaQtikj4/J8bNk+OJoXTscdsE9IlvMsFPxq/Uoa7pUrMGSeZU2eKfXoGsmuGRFfszi9aJKgJuf6Ky9VmdH9AJzYJNLJCIu311fo4CnS98eqwNbUMpAzOvlIuuIZFrEKlv08+5C6lkTloIAsGm3bKzJzjkVOSrxykmvRdYsqvNcK/uIFa5Yj6tlO9uudzi2i0hbxc62idiKqxA7UzWV/YzwWVl/KRkVrYvJqWW715qr3locxUmeXxbbyrCHkqEdLTtLTA1s3FWRurPk20uAcjcgzouGK9on1wP5FPOwnYe6ZmwS4FVyWhUdfaqjdUmd/cUeXDscdKEIbH6GnYpfzeJt9tbn1PQS2FjGPime6rxX93j1Ohg1uo9IvF54zLv5iZ62IfPzEb3AlJzpJRLZve+ur1HA06Vvj7iY7dWlDMS8Xi5yKQ7qKFHsoguugc0VCmiw6AOBDWwmoskmpbl8SlhgLe/E1fmQy79E8S6W7WK73uHYHoi0fcbG+mgSYocZm5z1dGo6MzbOOZyCPAr01k5b3af10tbM2ETdrYmZlDbTPxbielc0qVfGJgLUlhy0qh7qWqkoyNioOsCUGsFrMitbs3R46kBFOxx0oSNj4xn2Kn7N2LiWkKZHPTM2Tv46xivXIcjYbIMeGdtI6eZYNKKtbZyd0EskGZvvrq9R4Op+cKjtzNg6Shmoeb2/IjQin7Gxwt4r+e3kIGMDW3MfyppsVprzp4QF1uoBnwSO4rn4ios9u1iPc1Nnux46totIW8XOusbGFSJJiC3rXbmssdFZ6Y3eucam2yNRkAd6a7oxzG1+5TO2oIeyClhkbBI1Ve9OUvd3YtG1x4Fq3wRK/c4eFML0hnqozxySrE5qa3LG9oZ2dUIDm/aVOjpcqb0823K1BbQLUp/ErbHJmptX8fvVvviz82n3rWhdPdU7ynnqeHm6OZS4NbZSu54Fa2xizT5C5xjRi2OMv0S6xua7qzUKRCF/Ud8eQWDrtqFvaMU2n0MnssamSVmWaBSXydE1tjoCG3iUblwfwmD3Qd+KZsnm9HSyS0uvku917r+eutab8H0vze1DfaG74XHi203X2tcBCnuwOwPb/Z9jW0uj/l1Z/Rzb7g5sG87GBLYcCnsAAAAAAAAAAAAAAAAAAAAAAABgw1HtMgtnCum2uK2JRZSIhMSzXBTsg294R++8Q/uOohoAgEcisDX1eSz7w0u3g8Dm1O/es1zcLcUwskO5g8AGAHiEMjbW+7AKnaXbLVfEh4y/nfpdAhtLuWedR3Cn1jr0cQcAgG3O2LKb4gHvpNuVwPjbCZ58xkY6x9SU2j0zNufjDgAA25yxsUB94kUn3Xbe5mz8rep3DWws5T4crLEFWmvn496CiAYAsOPYMiNhAABAYAMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAeMyoDcVSi+0xIk+5IHC7Hg3QwLP2O7FWnTNcKrhdz1ChBIAdHdgewtt9hxM1TanNZeOis007A//+XZ3L0hkzXDHVF+x0JND5A7AbAls0MUAZTNNUW4lUmqzncdx/Y0hr43rfg0ZVa4ZTrkc5j/0hWQ61n6XquwmXGtdk8EUu3kY7ZRxMpLwbWSfYVvbPVK83oddxWu1ltlAreiBeC7yDvOYiv1QMjmOV1I3zVgyp4b7Rb7ZJbSiVwVGGllYHpYfR01RO86vvBYFNM7rHK9QDsFsD22jdJir2453dGpEAMznG4SsaMVX2OBDfg+qecRfYoqaNQnaT/WuW+va1MfVQ4MDhdrbRKvrNj+q+5G5DDmHPZG/6bBM+XG+zheAg7lDFQakuuQS22oEKR6OaFvYVawY+H/Ww73Qqg5OgSXvae8+oaTcNT2lgkyroNpImUlcTALDTA1uTPsxRkz7qYnrAGRgHNmrCeVqJ8yo1Q7Bx0EYzyqcaNlRohieBjSJE4gKbRqvxPVPupreUcD4kcYSCYJbm9Gtvs4WiB4V9lr5uqcFW3LAdH5CTcurF1gw3/E02RT8aIscxThMp5tl/KTbPNGvdGZuNqQhsAOyGwHaoYvKEsqqSuxW1n/XVGZvpm1UzBNtCMjbOknx7zdiKZIsNEg7vOV0Ws6s1MzYXsrrNFoKMTQ8VZmwcq6p7LnLGZkyRsRlupBnbV2M0RB6cnJhuizmwmb7b6arAVmogsAGwi9bYXqM7SwlsMzbUSWCjdS6/xtZWMwReTYsTWgK7OZQU7VdlbLow5m4ss641NvpV1tj0vN1mC0UPqn65Tl9TF1LqFN1DBwuBbMWg63+8xraXblNlcEayuIzzQdpttF4ENl0Y5OayJAgA2MH4D/Z6kXvTZH3tNoaNOtQ6xopvRQFAYNtZgY2+9XwAeI4NAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADuSO/GbmAQAwK7iZx98+ednMQ0AgN3EW4sXV54yy/Pxyb+R5cpb0w2TzceX77JZS/rT38cLF/J2PVusPDMfL5w4tnxQPFaOfDo9d5x+/PwH3EYaNswvB9p11wYAALaFY+/96u33Gub1a/vvtA+3kldWPm6YV69Nnm888c3Qh/uOnF+6+v0n8/bywgVqcqn9zUpSbVHQut5/4bdnri/+5KXXZqnNf6Rho/bJx0UbAADYFl5ZsYnZ4i9MZtOxauvD1rm8caRv/uTBhqmRq94QuZrkc/PnzLHl+ZPzNhublmwsJ3c6cs1j9z3X8I/3lpaLNgAAsC083z+7b2bgyhdX999bHG99tFjJG9HAlVc/kMD23CdLV784k7e//mtaG3rz9fN0TzrO2dgdm7Hdvb54d9/+SWozJQ3nFi5kRRsAANgO3r70/pOm2nr/3WleY/vLU8ZmbJfipXclsJmX/hEv/pPW2BZO3Ju+/Kf2zMpxuc187vz03JUjnx6Ml57lNtIwPm6yog0AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAI83tZfLxuTJt9qn+sMv59feI4/j1JTimAq2mWor7i/Tq65qH1SsVze6f6MB2SXbW9HtGdXwzVJTG0pxoQAAmxrYjgz++NoTa26NmqZ2YPwFG5booKXERKOH91RMnnae9bTdetSGvIZrVO8ryy5Hb9umpT+MmIyDYZZWB8u4TgCAhwhsz380v3SmZFMm97u5fvJUf1lcDWwGNfi/+bkTsuWZy38/uHTm2PLBuebkv05Nnzr3f/auLzSqKw8f7p2HZe7N5c5wZ8YEBhIYWA2BDZiYlxLWEIKLPggVWSYRVzPzYCExYDZpjG4hD7su+lJTNy92EWz7siVVLC6o3YJI2QeRsg9lu7BvQmVdWuji+/7+nTN3Jn+cxH9Ffx91nNx77rnnHnO+fOc3zffhZdjR4U+mkYiMKSETJZFXCeFdx46lIpFXE+RrvwhyjBpNdeaRFIHYHsBraTbI7Q6J2I4orykUii0SWy/aewfmYN++rsgrT5vr8t4kD4Gr4hsDZ2++hVvDP5jl1TE6E3/824PXA++TsX1dE8YfDo0lthP/MUxscQTdEnMhxZWQqYiz1hBbx47QNroGxJaDP3BxKZsb9QL6Avejug9VKBTbUmwflOr1PVFuofbOOXm/b+ev4RxuUq9TOSwCDqvSmfjzPtgm4kbxswIT2+n6YpE6MinFRvvKJsXmZQSVkIlNNpnNii2OvAD/WMUWJcpsCoViO8TmD58/tEAEYt8DY+HuskmxLdGZC8M/gFY72qTYzh67JoqNamxISY3y2doamyi2Uta+T9XYQO49eRLCsURrbAqF4lmIbd+l2tU/C7HR+3s9E3gOa2y3scbW9dGe08el1f7F08UBrLE9mraK7cvbtsaGn2XiThRkmQfKLJEPPFszEJDYMOSqMtUbcSO4hj8VjZDg5HwlhC/pI1KFQqF4zsCtqEKhUCixKRQKhUKhUCgUCoVCoVAoFAqFQqFQKBQKhUKhUCgUCoVCoVAoFAqFQqFQKBQKhUKhUCheb/SHudE3fQ78QXRJVygUzw8nvjp55ep0W03F+nFLa3Yoz5ksGzXw8FwstkRkNFnaeI37PZmt+ekmEd68sI1psf5xeEtyU9oc8XfkRBxtPAs0gZ0wG2t76+iSWyRRe7ez/eGV6NqpUCiacWjh9sDBX7TXNp7bsi8aukc+nVfYIfzpxPar/NbIFfpDO7ftGFWKMTkSnH37lNb2Idaducg28wqbDrfVQX3z/tRzRaFYH3u/GIPXw/XF2uX5VGAL+kfGBV44ceHoakj0g/bdCQkTeL2DGuXIznNoEhmjLEL5EOHyjssjoiRgJTMT8WFSb5HPTuGUyQd/Y7ieLFRLbAmdIq0V27fCqV45zzl99kQ5j56UFNIH7+FirxLa9jH1jPemTEAaIF8j7ehK6K/7U7wC32TZqDy0/MrEhh12Z/F6tsBE63IcOAosMQpmYvPwuZFPC/LEdMDyVa5zpUBP2dEVoJQsT/ZitzI3OFZqmL4P9SUT4kablf6YJWXK4RVGii1z2CsOLROhFi49GO9pR3UqFK8PPPmOT4KmwJZmYvv9z/t49e6nde8XeUX5g6SGaGMEqwuWVYzE5v/pwMwgr3P0CSe9w4fzcHUsxIaER/xQmo1cZlUPEQj2nuAp6gNe+iUjAVZsJcRb4mWyuktZITa/CLcqZXOdf3XtS1nZB0OPdoBoPW7bOe6ArkftswixWZHVa7kThh5gG0dsMPD9WZvTwPyCD+UV/GIcyBNP0gEr+nK9ONvIVfcGsbxI/wCBnRueWkNpEe4+1JebEDda7s8l4sD1QmzObR3b0aP6RaoHqAmx4s1TbEJsjcAWohggtlr94hm7l0xIQlm/biE2pxNIRiCxVUHYWcWGukYUGx5G+RZz3wG/egEmtzTC+IiNsHc4YaUhMF1DseV2T/XS0HaQMMI2Hle34oDWdWl+h1Vslp+40iYDNMhpqXYZR2yyn0w4bUaIDS5GxUbEhqQRy+144Fax4Rm8G3aV65zpKdgnnimybBVi65wZwsga+MkQE犀利士
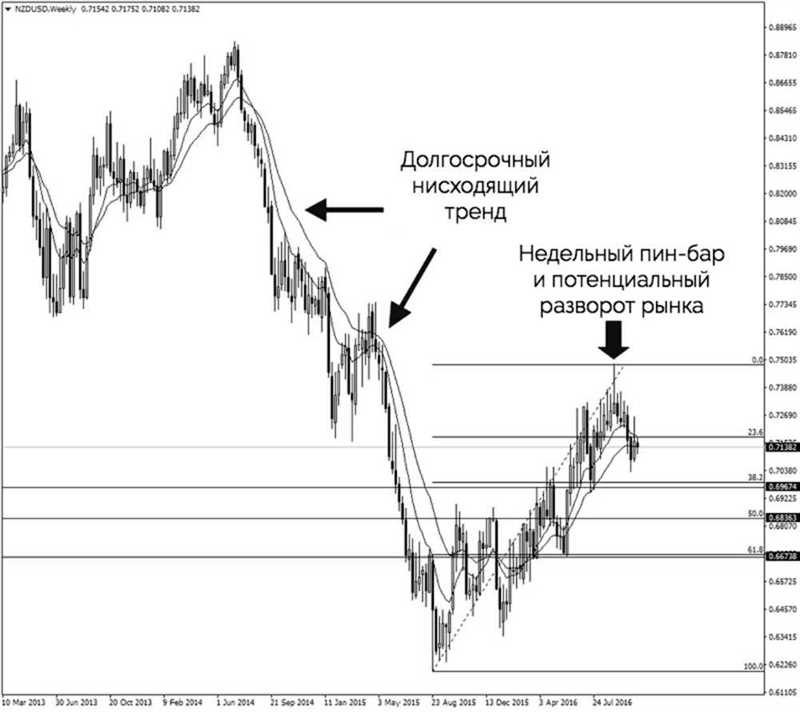
LHR9TI3rgOTvo+PfTUmJNNMbKLY7JSzFOVemdjgP/uTRL/XFW9Sje3u7QHzs76GYluyUS6i2D57VxSbrHtYObyjYmKDFl4Zli9IDBAFSGyzWWICq9g4k0UO00prKDb4+7tRs4bYGgIFk/ugZ+jLc8RWpZIZqBCSaE7JMH2AioLGtj0qNkoDZAagAcJ9Xbs2FBvLrXUUGw9cdGOrYiOFiE/cotioxobyTIgNd8QFmZuNFBtcsZFiw128nduUYqNehdhyfzmQx3/MRIlN8UbhxMLJK48GmNgagS2W2Gr1y29jje28FKzjICE1RDUr2oqe4+JT9/g/SOZg8AoQXzlPxEYLEDVelQ9T9p6k8VGxyGNtFFMxyOkVV1jDYl33+HyXUB/X93B3eK+H6lFwYJwX/JEuykdNkFGqtj32TDoG/yrfwnvd6Q1IYtLetJnYDNWmXI1tHgkU58ERG97O1dho4DBrdLWrscFDUY3Ng5HTjeiA3bzjdHiVpfdoL43EBs/4fpGnLFVjS9+H+srHqRpbkSaKqRqnosDXp4iNehViQ5b0qcbm6cenijcS2/mMbbOPAo1p/YjTrf+1vfQ/46rj0n2LLGnzM8b1AGJrdCutN6/Nx1E7/6Na+8Ntrz9WuOGzTINCocS23lodyrdBbM+hsr0usZntZy1v8crNn6B5Fp79pu32h9ovMEpsCoVCoVAoFAqFQqFQKBQKhUKhUCgUCoVCoVAoFAqFQqFQKBQKhUKhUCgUCoVC8ZyRGzWe+vkqfjLfj72ZzMXjr+jm+Cvy4k9L1mYVMqiIrdmk2IBTDsCIuCCxwUcpS74W1IB+wTKJXvU0RjTQF2lUm2wvvYFnsPuFp8Ukmr6g+AkR27GsOfyqfKOZ2Iiz6De1/WFxuWVbtCRlGG7t3Urimeas2Mi/51X/mrc/PBux4dKLsz2Lt83dbYQ2KBSvH7HFNwbIh9Ar549+nbkxAC+X3waSWV4Ncwu12v19l2r1PaSLavXFYh+dNmf/Vl8sUEBC9av6ydqjlYLJ3S3nDy3UFssj5BPCjrzhqU9REsLrF48pWYHO5W4+bCg2IjCxWGRiQ3/coRlhqw2JzQs6ds4TK7JXZRJ446hqyFeNjNhW8CBHCKBn3DwnNFAOQceBvBhoiykmdI1tsjRyCXKIUmEJlD7AeQWiggopKRRz6AuNFSeTExVAyLFb3E6051xgY19OI2ABFpPxeEb85yqhpDiQxXCR3d3EUS73ZMGGHbDNW/kWPeG4jZsIrDTj7IlUGEU8l7FjxZ4r1S7xHSZrPB6+GL4llLZ1hFMYkoxLqLAzhE7ypE75cg5TSFhEG/Kok1iJgimdcwkT6Gon06ZQvLSt6MdnjBDb5M23zK7csePAdTPDSx/BN/MuNMgdGmNLI2h1YXiKTg/4Q9NxwVBAArGjVzj4/TdlNP/2moit2vWhWV6tdk1AV9aA3JiD//png9jIXEcMG51iM7HdPYl/ttuKlvPGKjY4F4j084IkEqtZY5yRIx5kQ1rUUuyRy6626xFbbB0fpVOy3rVhCZQ+YPMKOFXAJT44YqPL++dC/MOxCC4iAVuMWqJmU18aKoU2dOyYYq9dsgKmkXP32Iy86niOhdhGOHirP5Qn5kc0Rp7cpIYGw4d/J/gJIAfYyA37sYENDPLdxAGx4Tva/JKjbwuxzcEkz5F23M/9xQHPEadI0KRxnAXG4Ozmq/y5QYN/FIqXqdj2ro6BFqtFQGHDIbvGXhheeu/chAGhVV8s52/93Sm2L2/z6dD7vC8ufEABCbLolq+ulPOnhqaR2KDhBCqHTGUKzp09du0YrSciNjzXVGMjqZZSbJyX4BZdi2LDC7jG5tzd8NXDL12QU6YgDrWBjRCwsQQ5ySHADXAsyQs40u5sKStxB2yPSfkMqbAESh+weQWUAVpMpe6lFVv/Y3ia/pBjETipAHMJwiZi4xwD4nTPKiNJmRHFRmoIuYOJDXsfmsF642TnJG8uJbSGH462qh5cQ/kzI6kwCsp9uCNjBT7igBpiph7JJZVoCSLFQZtQQfEWzTPk3YGJe+yIjUiP54hTJFKhFuxETKkU/i+B+B4Mcv4WQ+Wb4oUT2woQW2CWb6yUJ0GN7Tr0oyi2b0DJ/dEsl/P/ftcpNuAoOj3wfYA7MwpIYGJ7/9vzaGJdMKzYjq5WWbFdmkDFtpBWbEdXx0ixYUyMjSOgRVKRGpsxrcRGmjIOpI7F9GacbSUpNoxzKueh/5ITOnQwpdgooUFyCGDJjacUmxeQYuONmcvuS4UlkB23zSvgDNBmxeZqbP3VA7/LArFRLIJkaHmo89ZVbNykdI1GxYkMpJ5aFBt/gdeWrqUVGz1xSrGBsETFO5IKo/BaFJtIYmEmHLnP7XC2mNhmOfFGfgw0ZsiL9j8Y9ByxUZgCzxGnSHAKGAk1tE0fpsDGyB/07oz6qtgUL3crevEIarGLx2GR/ObrzI28rbGd+vbM3sV3/vu/mdVQiK1WX3w0TaeTyxiKwAEJTGxXHsJKunXxjGHFVru/psY2ZhVb7f6hux8aFgrAZSQgUp+KNoiNPxmgdHT8YU+bULxbK7FxjS0ucI2NPP+tnuFUzqYaG+cQGNPYilKolg005RrbLOUzhC4sgdMHZiSv4P/snU9oHOcZxj9m97S7M51ddleuQGCBDooRZcGr1WUxrBHCoIUIEoSRZRdFWh0KsgVyZFuKGxCltreHEDuyLza0qDiHGjmOiwN2qS9xDsW0dQ4BH0ouRRhSfEhIoLe+f75vdteWY9k01nr1/EDrmZ35/sxY8+iZb+b93rQmftcsCU7YJLOp6A31mz76Ug1hE91pFjYd1pITINkdJDvCnGRkEFGKxthcnj5Np8Bm1I6xiZXTI9ZDNMY9X/5waH8jGYXN1WD7qj7tw6EWx6b76dmSFD1Ja/fiT5whj1WrIWyHXIrXHs0i8Y2eNBnO0zE2yUoRG6TDh7CBHUzrrNfPmNn/qdzuzt09J8nc8yYyb+ZZ05jbvwc2+crWq8v9NOfrWUf8Iof68v9Z+R85aV0J/DYDoJdjd3wLYhE+/T6XfTOkXYUtveeneo8MwgYAAAAAAAAAAAAAAACgbbAB6gAA0EF4eHccANCucASzBJDrC5wahJ20W/S9UfqQNzElutqFeGPKCABA2xqvnLgvfQ9MQrU5VtFFlmu4tZfUaGcjby7ZEO9X8qIUAAC8BDZ02s6mkzNREHaPhgpOc+xQTuNqNPbJhnhD2AAAbe7YNLzcBWFLVHYicmzGRjtr8LQN8YawAQDaFjvGFuY4dPyiBGE3OzaZBCfQMTYNnrYh3hyrjecHAIDXl02m3sZTUQBApwkb3mMDAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADg/0562HgBTgPYyYw9PmfM6Yf1duiLz1O/yaQhXQme9bIvxdMmhfH47gTPGufC7nkepd0J/eRJl/pSEqIfBkZ2DXliTFsjJyO3My/lbAHOIx+PB7yFivEyNxi++FQlPk/aFNo6nyC0k6zntudEZvnUbU0DeU4qXAWg84jt+50Z/2CgHbrifZpvCFteZrdkYZPZLUmIdPZyk54SJeGUC15OZ8e0wqZZGHhK4DDXImwySzBv5bK6zQmbrfPF8zekp44njSv/pK5xEzwRZ7bNRQOThYIOtmxvf3vQ7/7bUXPhWDB2++7d+yZ78Z9L983CtbtX3/W7AxaYbJJFIX1qZub+2OO7tWVWH2+ptnw1tXAtfv4d8/apmeWezC+Xly+f+KJ2bObR/FDmQDfZhusztd2JrKaGkSoOfHFs6TcD/Pmz2vJS7R3Z5q+eEbE5QddZk7CRj1JVousvNjRvZ06y5kqELal5GeZV2MTxidboUiRsMkuwiJdMEfy0sHGjPOEmO7DAWi1azHHD+yaoV2FPRpyQGr+4SxBhRp1dI4eZ44JslbT1mFVpPoNcniW4L8XfhH+hPsQu2op4Uk+1nrnog1PmSCcktU6Wd6DqqI2+iW7rMWV+UCnKKXaSRvLx6GJTS64etWaajKfrrD3Inoz3qcvRk9Tj4oPmWvsmnORRo+o+/ywt66pWIcse1UIVswWms+VpXgx3zLi8wLYx+/D4zaLf/1X5o/6zgXf1aPrbevaDgYX3T3RfMeO5FmEzbxivZ3qqLomqaDFz4NRh2uvC+gjJBa2ODZgbuiN5rPAQTyf+b1prFrbwZvH0rXJ4k/dlY6Pb/vCuKoEXtAibl4wcmwndLR+t00UYaP6FFsdGGsLaFFjdaggbXZc9GRG2WN6aM1YPuuJDFRcq41kjR8aPZIe+4D74u1aGMqxuF6sZnUWdPFhs0DSrod71eUmqmgryPn7/WVUiETf/sz9l+IeTSXxm5UaqtxXpNOy2bhYH3pK362xDp4f1hLBe0tfpYSmVi4qS0tMmyceji80tuXqt0vIHraq6d7Eq0aqWst1hEzeaiLycbBialv2pZV3NSBUTuhwbunSYllqFzR4zri6wffzr92X6hT2yNv+IfseXajWxUempT/bM1GqP9vPf6b5UVrzBwrUa+bJLvTORY1ubIxU7PZVYGDpKF8noL9jLqbDNr6/sSx3oP8jCNlO7mx/QKljIbiRVzkTYZJsdmIoy/7U4NtWOaKpLcWx638mXmGQItMLGghVs4tj4Yhua/hHHRmt6u7o3FQY8vBdPspyR86Cm/V0Tu+a4MO9C3WsWNicx1G4sz93g1uTqz0eOrXo78O5USdjYkbIdirNacfebhE3rFmUWsbRtSWoddWzsrfiIVdg0B49LTcEKFk/qUYVBc0u2HnZefSn9Y6ASJJIu4pfUUtIdaUqErVslX45n14qcfGpZV1NSxZwus5sL9C9FnzRKf2fcMePiAtvH9R6+Fk/0/+NKlhzbCNmyyLGZN1ocW/acudCTGb9ZdI7N3DizOsmOjTSKvdzBMefY/vjVQSrGo2Ti2E4/rGsV4+LYrt8sNhwbbWPHJh6BFI18HumLyEJfyg2QNQlb7P2EEzb6EWvGLVotU2HL5hqDXSo8KmxcNrvJGJtzbKF4JJE+9iLk2Ob2pvxdxxP2PvYpx+aEjW8UI8cmbizvxtj86vRwYYKE7XhgLQ21Mnqctmzm2FwOnUuyrql1qPKtODb61zq2ppaaHFv657fF/NIpj+1jVSIxHmp1bNQSL1nHJn5zc8fGVTjHlveCbNBwbCyD7phxcYHtIhu//Jb8/l64ejQbjN1ejl8dyR5aljG2Y0tXWoStsvyr/3z334fv2VtRcneX35IxtvD8e6xzj2cuf2mFrfcMFVvpnTTWsd0ZaIyx3Rn4LX2WI8d256Mb56xOeDJQpeM37qloQ9isRvWK6dEhKr3n5K+SNn+gfSoaupzPVEu26TGq/W7TMbbFuNgOHjv6e2+g4pSeOtGdtLYvlJqbhI19DY8kSWfi7PXkxlRTT8uwGwtbJkzSBwlqQ9hEPJuFTYf0uu2QGh1MKON53PI8SX2XG2NLWWFzOXi4aNaOsYU5XWxpSfusZ0iT8egAGe15yG2VUtwd6sDuQy2OzURptFVSdVWrkOWQx9joF8IKm4zD5d0x4/ICbSV2bZOnhS1Fg9HE1ksWXuR5nx14kzvHl3lQmHZ3qlsl3MYz3JVohyoA2LHCJkNOrwQVmlclbPQzI/kAAATWSURBVDzeBWEDAAAAAAAAAAAA6GBGE3icBQDoMGK98ec9O8gibhoA0Gm8RMw4AAC8MuRFzGQU1CzhSTIhT1bDq+lDIh/1VU5+D8TrS+FxPwCgze3XsDFRUDPHcpvw80ENCAz5xff9Gjkjb3gVFlOGf0LciwIA2l3YNKh5j0Ywx/Ic6c1ToGXdBDYuErvwDQlfAcIGAHgdHJsLajaGZ+jRec7Esel8Yl7PvIRHFyaqv05A2AAAr4Vjc0HN8YAnwPCSHEmu8dg5HWPT8OhCystxFGZXArMIAgDanKceBoRB9Oxzk+BJPBUFAHScsOE9NgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAYCfjV4ujdZwGAHYmlVKpNPla9Xj2u+JWdhsvrRXx3wvADhW2SZPeO/I69Xh0EU4MAPBcYfu46K+W1kfI5JTK8kE/pXJhxF+dNLN/LZ2k2zraszDCO1fY4NHua6ul0vpEVU0R7VSabNRB+3MxMYOVMtdPZU16mBRU7NY9rl52n/2em7QV0Pfn69ZElnULfV8298rUYDl9S62lX50f5F3WitrBqL+0L7XGbVDbhtodZ8vGXS1WuOJKtA9v0cIAgE69FaWLfrxsKifNRr0iKvM1axEJWWWRhGwyPdwkbCyC/fXxskqi74RtUFKscjVch1/9ob9OS/6DEdMsbGb2zQcjtqay7G6b0gqoQtE92jY7KFt+eDBCdWy8WZz9vsxbB6UtXyrZqGsHXX/l28phKUFaSBK3yDVzV2lr+uNpWtN9ZIsrDADoTMfG2lFXGamwkSK/I8I2x1IzXiZhW2WDxD5rkkSEvtqo25KyQQzX+Tq7rrJv66Bvx8sibCVbdm2apO8e65kKm+xOUiViIxWQBqnylNjL8Za5Wyy7hSP10SPSMVYisXvk0ya1g1F/RSAr5+vS9wr5ssIcf8Nd5abWV742KqK6RY8OANCxwiYWrHKS7FJFjJF1bF/WSTf66+rYRuvPcGz87JFVqNrFxk/q2NSxbXwybCp3Go5to97q2PzqpYZjSw87x8a7r3w+zPePLIOyO6srrUoHo/5ax9Zft45tcTLd5Nj0Q/eRLVIY//0AdOytqA6arc/dKvNt2q3/tWvHrAkDUQDHH3bJ4ifIkE3oXpy6ZMvYyangHHBzLgiBjC7p5nT4Nbr6AUo+wtGpUz9Be+9OSEy1WNpKE/4/8IjemTue8Hh5OH0P2Wanz6E7Vw3tK7ZWj80t2t4cVmzTezfz8uTv4fJdqnVUk9hCxebSls9cPrHp8tszemy6sT5ZukdlTWyajcbPr1rU+QM25019R8+l3dBj24YaLhxVT6PNOL/Gz/gv8/MD+H2+a/bNGQAgsQEAAAAAAOA/y1ZuKIgDgCF5W2f1hjAAGJQre00QAAy4YstrI7m1YqwtiQ2AfhqvpN1jq6wRuxD3MjOCA2AYrFnU1WyhNRvBANBPWe2s24ktt5IaEhuA/nooso1UhxXb0pajdDYnOAB6WrEVUmWtim1eSj4yIstc3z02CBWAPhVtJ//vUdaNO/0gjuNEIjdOJHHj/nLixijMhcvOnJyYS7pz3dtL9/ZfbR0d2zo6d+vkyNbJn2x9uYj8bOvLRQSffQC0ay954CyHQQAAAABJRU5ErkJggg==” width=”304px” alt=”правила управления”/>

Форекс брокеры дают возможность открывать позиции с огромными кредитными плечами (до 1 к 500). На свой $1 брокер может дать ещё $500 взаймы. Начинающие трейдеры по своей не опытности перебарщивают с такими возможностями и открывают сделки с плечами 10, 50, 100, не понимая того, что они “ходят по лезвию ножа” в прямом смысле. Психологически проще контролировать не более 7 операций одновременно, оптимально – 5.

Управление риском и определение размера позиции | Forex риск менеджмент | Трейдер Вадим Глазун

К тому же, многие открывают много сделок по причине потерь, так как хотят быстрее наверстать упущенное. В итоге, это может вылиться в еще большие убытки. Суть такого метода заключается в том, что риски определяются размерами волатильности.

В расчёт не принимаются многочисленные примеры западных компаний. Альпари является членом Финансовой комиссии — международной организации, которая занимается разрешением споров в сфере финансовых услуг на международном валютном рынке. Если же вы настроены серьезно, то нет иного пути, кроме как позаботиться о достаточном для ММ депозите и работать так, как и должен работать профессиональный трейдер. Холодно оценить риски, знать свои лимиты и работать на результат.

И при таком подходе вы сильно уменьшите свои убытки. Есть минус – вас выбьет и цена резко вернется назад, но исходя из статистики это случается реже, чем вы используете эту «функцию» ограничив свои убытки. Этот, казалось бы, сложный вариант управления рисками, по мнению профессиональных инвесторов, является наиболее оптимальным на рынке Форекс. Пост – призыв задуматься и может быть пересмотреть свои риски в сторону уменьшения. Волатильность возросла – это хорошо, но и риски повысились.

Главные правила мани-менеджмента на Форексе

Но для серьезной работы такие суммы не подходят. А теперь представим, что соотношение было хотя бы 1/3. В итоге, соотношение риска к прибыли составило 5/15, то есть явный перевес с точки зрения профита и даже с учетом комиссий, вы все равно остаетесь в плюсе. Как видно, стратегия, которая даст вам 50% прибыльных сделок на дистанции может оказаться профитной в том случае, если вы будете правильно использовать соотношение риска к прибыли.

Допустим, вы будете https://forexinvestirovanie.ru/, вкладывая в сделку 10% от своего общего баланса. Многие новички любя отыгрываться после неудачной сделки, поэтому вкладывают в следующий контракт 50% или даже 100% своих средств. Как итог, пара слитых контрактов и спекулянт остаётся ни с чем. Следует осуществлять регулярный вывод средств с биржи. Это позволит отчетливо видеть полученную прибыль и понимать, что стратегия выбрана правильно. Это самая распространенная ошибка начинающих трейдеров.

Конечно, мы не говорим, что это априори невозможно. Но достичь такого результата крайне сложно. Затяжная серия неудач может случиться у каждого. Но если вы будете заключать сделки по 2%, через 5 сделок «вне денег» вы лишитесь всего десятой части своего баланса.

Естественно ничто не мешает выбрать другое значение 1%, 3%, 5% для своей мани менеджмент. Не рисковать в одной сделке более 5% от общего капитала. Открывать позиции только маленькими лотами. Если сделка оказалась успешной, то докупать ещё.

Что такое соотношение прибыли и риска?

Ведь не будут же всегда только убыточные позиции, в какой-то момент придет прибыль и вот тогда все убытки перекроются. Для того, чтобы такой метод работал, необходимо иметь безграничный депозит. В противном случае, вы рискуете потерять все свои деньги. Эта часть мани-менеджмента связана с риск-менеджментом (управлением рисками). Трейдер должен сопоставлять размер лота с величиной депозита для максимизации прибыли и стараться не допускать значительного убытка в случае серии неудачных сделок. В значительной степени, стратегия, которую вы выберете для своей торговли, зависит от вашей личности; это является частью процесса становления для каждого трейдера.

• Для расчета Risk Reward достаточно соотнести размер тейка и стопа в пунктах.
• То-ли дело низ таблицы — вот где прибыли, вот где жизнь с рынка.
• Кстати, сам Ливермор заработал большие деньги, нарушая установленные самим собой правила.
• Но такая игра является нарушаем правил мани менеджмента.
• Динамика капитала является основным мерилом и показате¬лем уровня эффективности хозяйственной деятельности компании и ее рыночной стоимости.

Одной из них является фиксированный размер лота в каждой позиции. Это самый простой метод, который только можно придумать. Для каждой позиции определяется, например, 0.1 лот.

Получать новые комментарии по электронной почте. Необходимо учитывать удобный режим торговли, не торговать в ночное время, если комфортнее торговать в дневное. Важен грамотный подход к выбору валютных пар. Следует выбирать относительно спокойные и предсказуемые активы.

В 1992-м Винс пишет книгу “Математика управления капиталом”, в которой он соединяет своё “оптимальное F” касающееся размера позиции с оптимальным портфельным менеджментом. Но мы добавим, что в нем также содержится набор правил и техник, направленных одновременную минимизацию рисков параллельно с максимизацией прибыли. Технический анализ позволяет вам устанавливать тысячи возможных стопов, в зависимости от графика движения цены или различных сигналов, предоставляемых техническими индикаторами.

Мани менеджмент, или управление капиталом, – главная составляющая успешной торговли на валютном рынке Форекс. Управление рисками позволит трейдеру правильно рассчитать торговый лот и избежать значительных просадок по счету. Без использования ММ счет трейдера обречен на слив (даже при условии использования прибыльной торговой стратегии профессиональных трейдеров). Если торговая система определяет точки входа в рынок, то система управления рисками определяет точки выхода из него. Успех в трейдинге состоит не в том, когда вы начинаете стабильно зарабатывать, а когда перестаете терять свои деньги.

Однако имеются рекомендации не открывать вторую позицию до тех пор, пока первая не вышла на уровень безубыточности. Выше мы рассмотрели возможность управления рисками, а теперь поговорим о еще одном важном аспекте мани менеджмента – потенциальной прибыли. Ограничивая риски, вы снижаете вероятность больших потерь. Но мы ведь торгуем не для того, чтобы только защищаться. Соответственно, каждый трейдер должен задумываться о том, какую прибыль он хочет получить, открывая ту или иную позицию.

В периоды сильного тренда это полезно для наращивания своего капитала. Главное делать всё адекватно и ни в коем случае не пересиживать убыток. Возможность взять в долг у брокера очень заманчиво. Но такая игра является нарушаем правил мани менеджмента. Вы когда-нибудь задумывались, в чем причина ваших неудач в трейдинге? Многие начинающие трейдеры ищут причины в убыточной стратегии, запаздывающих индикаторах или недобросовестном брокере.

Совет рисковать в каждой сделке 2% от депозита — это понятно. Даже те из нас, у кого были в школе пятерки по алгебре, уже давно забыли все нужные формулы. Дабы облегчить жизнь рядового трейдера, мы сделали на нашем сайте специальный калькулятор лота. Мани менеджмент позволяет управлять рисками, что очень важно для торговли. Это строгий и холодный расчет для достижения целей.